La criptografía está de moda. En el mundo de hoy se escucha
hablar cada vez más de encriptación, de conexiones seguras y contraseñas. Ya
sea en el cajero automático o cuando el explorador nos anuncia que estamos entrando a una "conexión segura",
cada día usamos
sistemas encriptados sin darnos cuenta.
Para los profesionales que trabajan en informática se va haciendo indispensable
aprender los conceptos detrás de las
comunicaciones seguras, la encriptación y todo eso. En éste artículo divulgativo
colocaré algo de la teoría y la práctica de los
métodos de encriptación más conocidos, sus fortalezas y debilidades.
Algo particularmente atractivo de la criptografía es que
nunca será una disciplina más de la ingeniería. Se trata de un
arte por definición incierto, siempre existirá la posibilidad de que un matemático, un linguista o un simple aficionado a los acertijos rompa los
criptosistemas más seguros, se trata de una continua guerra de ingenio
entre criptografos que hacen sistemas y criptoanalistas que intentan romperlos.
Para comenzar algunos conceptos de la Teoría de la
Información del gran Claude Shannon, mencionados de la manera mas concisa y
simple posible.
|
| 1.- Cantidad de información |
Se considera como información aquello que no es predecible, el ejemplo clásico
para ilustrar este
concepto es el siguiente: supongamos que tengo una bolsa con 9 bolas negras y una blanca.
Sacando una bola quiero predecir el color de la bola siguiente:
Si saco una negra esto me dará mínima información, si saco una blanca la información obtenida será máxima, ya que puedo asegurar que la siguiente bola va a ser negra.
Desde otro punto de vista, después que saco la bola blanca la información
contenida dentro de la bolsa es cero. Hay certeza, sin necesidad de mirar, que
todas las demás bolas son negras.
Conocemos más información sobre un hecho mientras mayor sea el número de posibilidades distintas de ocurrencia, por ejemplo si sabemos el número ganador de la lotería conoceremos más
información que si sabemos el número que saldrá en la ruleta y mucha más que si conocemos si una moneda saldrá cara o sello. Es decir que la información es una medida de disminución de incertidumbre sobre un proceso.
En otras palabras la cantidad de información es cuantificable, mientras más
incertidumbre, más información contiene el objeto, mientras menos
incertidumbre, más información posee el sujeto que observa.
Pasemos ahora a un ejemplo de criptografía. Supongamos que tenemos un texto plano (sin codificar) y su correspondiente texto codificado por un método que use una clave K para hacer la transformación. si
tuviéramos una máquina de capacidad ilimitada que pudiese analizar estadísticamente todas las posibles transformaciones
y si
repitiéramos el proceso con distintos mensajes cifrados con la misma clave, podríamos encontrar la clave más probable por análisis estadístico. Hay sin embargo ciertas claves que hacen este análisis teóricamente imposible, son
las que cumplen la condición del Criptosistema Seguro de Shannon.
Sin embargo estas claves no tienen utilidad práctica ya que deben ser igual o más largas que el propio mensaje lo que las haría vulnerables a su vez al igual que al mensaje original. Conclusión, el
Criptosistema Seguro de Shannon no es útil en la práctica y todos los sistemas
reales son, al menos en teoría, vulnerables ante un análisis estadístico como el
descrito
|
| 2.-Redundancia |
Supongamos que leemos el siguiente texto
e_
_u_stro ej_mplo
a_ter_or
no es difícil
deducir que la frase original era "en nuestro ejemplo anterior" simplemente lo
hacemos sacando información del contexto, de las letras adyacentes. Todos los lenguajes naturales son redundantes, es decir trasmiten más información que la estrictamente necesaria y esta redundancia puede ser matemáticamente medida y estadísticamente analizada. Esta redundancia es lo que se aprovecha en los programas que comprimen la información como por ejemplo el Winzip, podríamos almacenar, por ejemplo, los trozos de palabras
que más se repiten como un solo símbolo de manera similar a como hacen los taquígrafos, etc.
Otro uso de la redundancia son los chequeos de redundancia cíclica (CRC) que permiten chequear si un bloque de información ha sufrido o no cambios durante su transmisión (errores de transmisión por ejemplo)
Los ataques a texto cifrado por fuerza bruta se basan en gran medida en análisis de la redundancia (se sabe que letras o combinaciones son las que más se repiten en un determinado idioma por ejemplo), pero si comprimimos el texto antes de cifrarlo lo hacemos invulnerable a
esta clase de análisis
|
| 3.- Confusión y difusión |
Por definición existe una relación entre el texto plano y el cifrado, esta relación está dada por la clave, la confusión consiste en ocultar esta relación y hacer que sea muy difícil de encontrar. El mecanismo básico de confusión es la sustitución donde un caracter se sustituye por otro, para esto pueden emplearse métodos simples o muy complejos.
La difusión consiste en disminuir la significancía del texto adyacente mediante trasposiciones, esto se logra básicamente cambiando de orden trozos dentro de un texto para que no puedan ser deducidos a partir del contexto.
|
| 4.- Números grandes y aritmética modular |
Los números grandes son usados en los sistemas de clave pública para hacer difícil que pueda determinarse una clave privada a partir de la publica. Hay una relación matemática conocida entre ambas claves el punto es que es muy difícil de calcular, particularmente en el algoritmo RSA se trata de factorizar un número primo grande, hasta el momento no se conocen medios prácticos para hacerlo dado un número lo suficientemente grande.
Factorizar es un problema inverso a multiplicar, dado un número N se trata de encontrar un conjunto de números primos p1, p2...pn tales que multiplicados den N, no existen en matemáticas algoritmos eficientes para determinar estos factores primos dados ciertos valores de N.
La aritmética modular se usa en las operaciones de cifrado y descifrado por la característica de tener algoritmos perfectamente reversibles,
es decir que tienen su correspondiente función inversa lo que es ideal para codificar-decodificar.
|
|
5.- Números al azar
|
El azar es, en palabras simples, lo que no
podemos predecir. Nuestra idea intuitiva del azar se relaciona con
tirar una moneda al aire o la bolita de la ruleta, debemos comprender
sin embargo, que si creemos en un mundo regido por causas y efectos el
verdadero azar no existiría en la naturaleza. La moneda al aire o la
bolita de la ruleta dado un número suficientemente grande de
registros terminan marcando alguna tendencia significativa. Con la
llegada de los computadores y su gran capacidad de cálculo se hace
más fácil determinar estas tendencias sobre largas series.
¿Que tienen que ver las secuencias al azar con
la criptografía?. En los sistemas criptográficos modernos no se usa
siempre la misma clave, sino que se genera una clave de sesión, al
azar, cada vez que se encripta un mensaje. Es indispensable que esta
clave sea realmente impredecible, ya que si alguien externo pudiera
dar con la secuencia de generación toda la seguridad del sistema
quedaría comprometida.
Es teóricamente imposible generar una
secuencia completamente aleatoria (al azar) por medio de un programa
en un computador, a lo más se pueden generar series largas muy
dispersas pero llegado cierto punto siempre terminan repitiéndose por
la naturaleza determinística de todo algoritmo.
Para solucionar este problema y crear secuencias lo más aleatorias
posibles se tiene que disponer de un número inicial (o semilla) que
se genere por un proceso genuinamente al azar, a
partir del cual se genere el resto de la serie. Puede entonces
escribirse un algoritmo que partiendo de esa semilla genere una buena
serie seudo-aleatoria y que resulte prácticamente imposible de
predecir para quien no conozca la semilla o número inicial.
Para generar esta semilla se ocupa normalmente
las posiciones registradas por el movimiento del mouse durante unos
segundos, el reloj interno del computador o el "ruido
blanco" generado por la tarjeta de sonido; con cualquiera de
estos fenómenos se puede crear un número aleatorio que sirve como
semilla.
|
| 6.- Claves débiles |
Como hemos visto un criptosistema produce un texto cifrado a partir de un texto plano, la relación que permite cifrar y descifrar es un tercer texto o número llamado clave. No debe confundirse la clave con el password que da acceso al usuario para generarla, normalmente la clave es generada automáticamente por el sistema y en sistemas de clave pública como PGP es distinta y aleatoria para cada mensaje. El password solo da acceso al usuario para "encender" el proceso.
Algunos criptosistemas tienen, sin embargo, claves débiles, que generan cifrados de muy baja seguridad,
o semi-débiles que generan cifrados vulnerables, puede darse el caso extremo que una clave deje el texto plano tal cual y no lo encripte en lo absoluto. Estas claves débiles son, sin embargo, conocidas y existen mecanismos para evitar su uso en caso de que sean generadas
|
|
7.- Algoritmos asimétricos o de clave pública
|
En un algoritmo de clave pública cada parte tiene dos claves, una privada que usa para
desencriptar los mensajes que recibe y también para firmar los que envía y una clave pública, conocida por todos, que permite que los demás
encripten los mensajes que le envían, estos mensajes así encriptados solo él
pueden ser descifrados por el destinatario, quien posee la correspondiente
clave privada.
Ejemplo: Juan tiene las claves (Cpriv_Juan) (Cpub_Juan) y Pedro tiene las claves
(Cpriv_Pedro) (Cpub_Pedro), además Juan tiene
(Cpub_Pedro) y Pedro tiene (Cpub_Juan)
Juan le envía un mensaje a Pedro, lo encripta con (Cpub_Pedro) y Pedro lo descifra con
(Cpriv_Pedro)
También podría mandarle un mensaje firmado, para ello lo encripta con (Cpub_Pedro) y lo firma con
(Cpriv_Juan), Pedro leería la firma con (Cpub_Juan) y podría estar seguro que solo Juan pudo mandar ese mensaje (ninguna otra persona sabría como generar la firma de Juan)
En resumen es el medio ideal para enviarse mensajes encriptados entre dos personas que no se conocen y no tienen forma segura de enviarse una clave secreta común, por eso estos sistemas resultan tan útiles en
Internet. Los inventores del concepto de clave pública (o asimetrica) fueron
Diffie y Hellman en 1990.
El algoritmo estrella de encriptación asimetrica hoy es
el RSA (por sus inventores Rivest, Shamir, Adleman) es a la vez el más
sencillo, fácil de implementar y hasta el momento ha soportado todos los
ataques conocidos cuando se usan claves lo suficientemente largas (por ejemplo
1024 bits o más)
La mayor vulnerabilidad conocida del algoritmo RSA tiene
que ver con el largo de las claves, el propio Shamir presentó en 1999 un
método que ponía en peligro al RSA con claves de 512 bits o menos, hoy se
considera "muy seguro" al RSA con claves de 1024 bits.
RSA es un cifrador de bloque, es decir crea bloques de
longitud fija, si faltan datos para completar un bloque usualmente el faltante
se rellena con ceros.
|
|
8.- Firmas digitales
|
La firma digital sirve, como dijimos antes, para autentificar
un mensaje, o sea para asegurar que el que lo mandó tenía acceso a la clave
privada que firma. La firma digital se genera creando un resumen del mensaje, comprimiéndolo en un bloque pequeño de
longitud fija
La particularidad de este resumen (o función Hash) es que
resulta único para cada texto plano: no importa que el texto tenga varios miles
de bits, basta con cambiar un bit cualquiera para que se genere un resumen
distinto. Esta es una propiedad sorprendente pero está matemáticamente
demostrado que es posible y, de hecho se usa ampliamente para las firmas
digitales.
Esta firma o resumen se encripta con nuestra clave privada y
es desencriptado y chequeado por el que tiene nuestra clave pública. Solo
nosotros, con nuestra clave privada podemos crear un resumen (o firma digital)
que puede ser desencriptado por cualquiera que tenga nuestra clave pública.
Así, si un mensaje tiene nuestra "firma digital" el destinatario
podrá estar seguro que solo alguien con acceso a mi clave privada (yo) pudo
enviarlo. El algoritmo estrella para producir firmas digitales hoy es el SHA,
creado por la Agencia de Seguridad Nacional de USA, que se considera seguro y
libre de "puertas traseras" (brechas ocultas de seguridad, que,
eventualmente, permitirían a la NSA romper la codificación)
¿No podría falsificarse una firma digital simplemente copiando y pegando el bloque
de texto a otro mensaje?. No. Porque la firma contiene información (el "resumen del mensaje" o "hash de una vía") acerca del texto que está firmando. Si el mensaje es distinto en un solo bit del que fue usado para originar la firma esta será rechazada.
Así vemos como la firma digital nos da una seguridad mayor aún que una firma
en papel porque garantiza la integridad del contenido, no podemos firmar
digitalmente un documento en blanco y después llenarlo, como tampoco podemos
"cortar y pegar" una firma digital.
Incluso se puede firmar un texto no encriptado, como en el
ejemplo siguiente:
-----BEGIN PGP SIGNED MESSAGE-----
Hash: SHA1
Este es un ejemplo de documento firmado, sin encriptar. cualquier cambio que se le haga con un editor causará un error de verificación
al pasar por PGP
-----BEGIN PGP SIGNATURE-----
Version: PGPfreeware 6.0.2i
iQA/AwUBOfiSiynKvl3sv06mEQK5MgCdHJgD8Bh5sIJfSLPEg2HFmLdyen4AoMuv
YqwdJXq892sNh3xJL/pKo+L3
=5pIW
-----END PGP SIGNATURE-----
Cualquiera que tenga mi clave pública y el PGP `puede
verificar el bloque anterior, si le cambian aunque sea un espacio, la firma no
se verificará correctamente
|
|
9.- PGP
|
Aquí llegamos a la parte
práctica. Todos los conceptos vistos anteriormente tienen su expresión
práctica en el programa Pretty Good Privacy (Privacidad Bastante Buena) creado
por Phill Zimmermann, que es el estándar de facto usado para la encriptación de
e-mails, discos duros, comunicaciones de voz y muchas otras aplicaciones.
PGP puede descargarse gratuitamente de
http://www.pgpi.com y sus versiones más
populares son la 2.6i (para MS-DOS) y la actual 6.0.2i (para Windows 9x).
También existen versiones de PGP para Macintosh, Unix, Linux y para casi
cualquier sistema operativo actual medianamente popular.
Desde el punto de vista del usuario PGP tiene un sistema
muy cómodo para gestionar las claves (que es lo que más enredos causa en los
sistemas de clave pública), almacenándolas en dos archivos: secring.skr
(que almacena las claves privadas) y pubring.pkr (que almacena las claves
públicas). Podemos pensar en estos dos archivos como "llaveros" donde
guardamos nuestras llaves privadas, públicas y las llaves públicas de los demás.
Obviamente si se nos pierde secretring.pgp (por ejemplo si se nos borra) no
podremos desencriptar ni encriptar ningún mensaje, por lo que es buena idea
guardar una copia en un lugar seguro.
También PGP guarda la "semilla" para generar
nuestras claves aleatorias en el archivo randseed.bin, ese es otro archivo
importante que no debiera quedar expuesto al robo. Si randseed.bin se borra PGP
creará otro automáticamente usando el reloj interno del PC, igual es recomendable guardar una copia en un lugar seguro.
PGP tiene además la utilísima función llamada
"armadura ASCII" que consiste simplemente en convertir los archivos
encriptados de cualquier tipo en ficheros de texto ASCII. Por ejemplo un archivo
binario como un programa puede encriptarse y convertirse en texto ASCII que se
puede enviar como simple texto por correo electrónico
Una clave de PGP contiene:
- la secuencia binaria creada
para la sesión específica
- la identificación del dueño de la clave (nombre+e-mail)
- un número que identifica a la clave
- la fecha de expiración
- la versión de PGP con que fue
generada
- la
"huella digital" que es un número hexadecimal como, por ejemplo:
17AF BAAF 2106 4E51 3F03 7E6E 63CB 691D FAEB D5FC
¿Para que sirve la huella digital? supongamos que yo
recibo una clave pública de Juan Pérez y no estoy seguro si es realmente la
suya o me la envió un impostor que lo suplanta (esto se conoce como el
"ataque del hombre de en medio"). Para asegurarme puedo llamar por
teléfono a Pérez, por ejemplo, y pedirle que me dicte la huella digital, si
coinciden ambas entonces puedo saber que la clave que he recibido es auténtica
|
|
10.- Como funciona el PGP
|
Curiosamente, recién me doy cuenta que no he hablado
de la criptografía de clave privada (o simetrica). Bueno, esa es más sencilla
porque se trata de que tanto el emisor como el receptor usan la misma clave para
encriptar y desencriptar. Este método tiene varias ventajas respecto de los
pares de clave privada/pública, la principal es que se obtiene mayor seguridad
con claves mas cortas (de menos bits) y una desventaja básica: que no se puede
enviar la misma clave por un medio inseguro como es Internet sin correr el
riesgo de que alguien la intercepte y se la apropie, con lo que podría leer
todos nuestros mensajes.
PGP es un sistema mixto, pues cada vez que se codifica
un mensaje, primero se comprime el texto plano (para evitar la redundancia),
luego se genera una clave de sesión (aleatoria) y con esta clave de
sesión se encripta el mensaje. La clave luego se encripta usando la clave
publica del destinatario. Este paquete de clave de sesión (encriptada con la
clave pública del destinatario), texto (comprimido y encriptado con la clave de
sesión) y a veces firma (encriptada con la clave privada de quien envía) se llama
ciphertext y es lo que se envía por Internet. El receptor desencripta la clave
de sesión con su clave privada y usando esta clave de sesión desencripta el
mensaje, se descomprime y queda listo para ser leído.
O sea el mensaje se encripta y desencripta con la misma
clave de sesión (método simétrico o de clave privada) pero para enviar las claves de
sesión se encriptan con el par de claves pública-privada.
Si usamos PGP 5x o superior, el algoritmo simétrico (el de la clave de sesión) usado
por PGP puede ser cualquiera de estos tres:
- CAST: clave de 128 bits, rápido, bien diseñado, su
desventaja: es relativamente nuevo y no ha sido sometido a ataque durante
mucho tiempo. Tiene patentes pendientes pero existe el compromiso de sus
creadores de dejar una versión libre en cualquier caso.
- Triple-DES: clave de 168 bits, el algoritmo DES, publicado
por IBM en los 70s aplicado tres veces lo hace un sistema muy robusto, tal
como los otros dos algoritmos no se sabe de nadie que haya logrado romperlo
a la fecha. No está protegido por patentes, es el más lento de los tres
- IDEA: clave de 128 bits. el algoritmo fue publicado en
1990 y ha soportado toda clase de ataques desde esa fecha, probablemente
obtenga patente lo que podría ser un problema para su uso futuro
Por defecto se usa CAST pero podría escogerse cualquiera
de los tres con Launch PGP Keys, Edit, Preferences, Advanced
A su vez, según el tamaño de nuestra clave será la clave pública
usada para encriptar la clave de sesión
- RSA key pair para claves pequeñas, por ej. 768 bits
(seguridad débil), esta funciona con PGP 2.xx
- DH/DSS key pair para claves grandes, por ej. 1024/2048
bits. El PGP 5.xx y superiores generan por defecto estas claves, pero
también aceptan y generan claves RSA por razones de compatibilidad
Para la firma digital PGP usa el algoritmo SHA que crea la
función Hash requerida.
Finalmente podemos preguntarnos ¿que son al fin y al cabo
las claves?, en PGP las claves son números enormemente grandes, por ejemplo una
clave de 1024 bits es un número binario ¡de 1024 cifras! o sea su cifra
máxima es 2 elevado a 1024 lo que equivale a un número decimal con varios
cientos de cifras, solo como ejemplo, se estima que el número de átomos que
contiene la Vía Láctea es de 2 elevado a 223, creo que sobran
comentarios.
|
|
11.- El enredado problema de la confianza
|
Una de las principales virtudes del PGP (así como de
todos los sistemas de clave pública) es que permite establecer un canal de
comunicación seguro entre dos personas que no se conocían previamente, que
están físicamente distanciados y que no pueden intercambiar una clave
"por mano". O sea puedo establecer una comunicación encriptada con
personas que uno solo conoce por e-mail.
Sin embargo sabemos lo fácil que resulta suplantar a
alguien con un e-mail falso, esto hace posible el "ataque del hombre de
en medio" donde, por ejemplo, juan me envía una falsa clave públñica
haciéndose pasar por Pedro y puede leer cómodamente todos mis mail que
envío (según creo yo) a Pedro, pues tiene la clave privada correspondiente.
Para evitar este ataque, que es imposible de tratar por
medios computacionales se han ideado una complicada serie de validaciones y
certificados digitales para asegurarse que las claves son realmente de quienes
dicen ser. Así hay distintos niveles de "validez" o
"confianza" (Trust) en una clave. Si yo recibo la clave de Pedro por
correo electrónico, por ejemplo, y no trae ninguna firma en la que yo tenga
"confianza" la clave aparecerá en mi llavero como "no
válida" (barra de Trust transparente).
Eso no significa que no funcione
sino que solo indica que no hay nadie de confianza que me certifique que esa
clave es realmente la de Pedro (en el llavero mostrado en la figura de más
abajo la clave de Jorge Figueroa aparece marcada como "no válida").
Si, por ejemplo yo llamo por teléfono a Pedro y
confirmo que la "fingerprint", el número de identificación y el
tamaño de la clave que tengo coincide con la
que él me dicta, entonces tendré confianza en la validez de esa clave y yo
mismo la puedo firmar (Keys, Sign) con lo que la clave quedará
"validada" con mi firma y alguien que tenga confianza en mí o me
conozca personalmente tendrá también confianza en que la clave de Pedro es
auténtica. El mecanismo es bastante enredado pero todavía no se inventa un medio mejor de eliminar
el riesgo del "hombre de en medio"
¿Es posible que alguien genere un par de claves falsas con mi nombre? claro que si, cualquiera puede crear un par de claves y ponerle el nombre que se le ocurra, también, si tiene los medios y conocimientos suficientes podría replicar cualquiera de los otros atributos de la clave
auténtica tales como el identificador o la fingerprint (huella digital).
Si embargo no es posible modificarlos todos a la vez, así al verificar la autenticidad de una clave (chequeandola por ejemplo por teléfono con el dueño) debemos comparar:
* el identificador
* el fingerprint
* el tamaño
Si coinciden estos tres puntos podemos estar seguros que la clave no es falsificada
|
|
12.- Debilidad del párrafo secreto en PGP
|
Actualmente, el mejor ataque posible contra PGP consiste en atacar con diccionario buscando el párrafo secreto. En este tipo de ataque un programa toma palabras de un diccionario y las junta de diferentes maneras intentando adivinar el párrafo secreto.
Por esto es fundamental escoger un buen párrafo, muchos de estos programas son muy sofisticados y toman ventaja de los dichos, refranes populares y reglas de la gramática para armar sus frases, las frases de una sola palabra, nombres propios (especialmente si son famosos), frases célebres, etc. son usualmente crackqueables por uno de estos programas.
En http://www.voicenet.com/~markm/pgpcrack.html
se puede encontrar más información sobre uno de estos programas que intentan adivinar el párrafo secreto.
Algunas características de un buen párrafo secreto son:
- Evitar el uso de idioma inglés
- Mínimo 12 caracteres
- Incluir letras, números, espacios y signos de puntuación
- Mayúsculas y minúsculas
- Frases que contengan palabras indígenas o poco conocidas
- Evitar significados convencionalmente conocidos (frases o nombres famosos,
referencias personales, etc.)
-Evitar a toda costa las referencias personales a uno mismo (nombres propios de
familiares, fechas de nacimiento, número de teléfono etc.)
Siempre existirán métodos para obtener párrafos
secretos sin recurrir al criptoanálisis. Por ejemplo la "ingeniería social" para averiguar las claves, captar la radiación electromagnética de los computadores
(los ataques Tempest), el chantaje o por ultimo la "Criptografía de
Goma" que consiste en golpear a alguien con una cachiporra de goma hasta que
finalmente nos diga su párrafo secreto ;-).
|
|
¿Se ha podido descifrar un mensaje con PGP?
|
Se han roto públicamente dos mensajes encriptados con RSA
(el algoritmo usado para encriptar las claves públicas)
Primero la clave RSA-129. Los inventores del RSA publicaron un mensaje encriptado con una clave pública RSA de 129 dígitos (430 bits), y ofrecieron U.S. $100 al primero que lograse desencriptar el mensaje. En 1994, un equipo internacional coordinado por Paul Leyland, Derek Atkins, Arjen Lenstra, y Michael Graff factorizaron con éxito esta clave pública y recobraron el texto plano, que decía:
THE MAGIC WORDS ARE SQUEAMISH OSSIFRAGE
Ellos encabezaron un enorme esfuerzo voluntario en el cual el trabajo fue distribuido
vía e-mail, fax y correo a trabajadores en Internet cada uno de los cuales procesó su parte y devolvió los resultados. Se usaron alrededor de 1600 computadoras, con diverso poder de cálculo, desde maquinas de fax a supercomputadoras Cray. Ellos usaron el mejor algoritmo de factorización conocido a la fecha; desde entonces han aparecido otros mejores pero los resultados son aún instructivos sobre lo que costaría desencriptar un mensaje cifrado con RSA.
Los coordinadores estimaron que se gastó unos ocho meses de tiempo real y uso aproximadamente 5000
MIPS-años de tiempo computacional.
¿Que tiene esto que ver con PGP? la clave RSA-129 es aproximadamente igual de segura que una clave PGP de 426-bit
. PGP recomendaba claves de 384-bit keys para un nivel de seguridad "casual"; las versiones modernas ofrecen un mínimo de 512 bits para sus claves.
Note que todo este esfuerzo logró descubrir solo una clave, no un método general que permitiera romper otras claves.
Para más información sobre el proyecto RSA-129 project, vea: ftp://ftp.ox.ac.uk/pub/math/rsa129/rsa129.ps.gz
Un año después, por primera vez una clave real de PGP fue rota. Se trató de una clave de 384-bits que fue crackeada por una entidad anónima llamada "Blacknet". Un equipo formado por Alec Muffett, Paul Leyland, Arjen Lenstra y Jim Gillogly se las arreglaron para conseguir tal poder de computación (aproximadamente 1300 MIPS) para factorizar la clave en tres meses. Luego se usó para desencriptar algunos mensajes de dominio público que se encontraban encriptados para tal efecto.
Lo más importante de este ataque es que fue realizado en secreto y no se divulgó hasta que se obtuvo la clave desencriptada. La mayoría de los computadores se usaron durante el tiempo libre y la potencia computacional requerida estaba al alcance de una organización grande a media.
Estos ataques han consistido en determinar la clave
secreta de alguien a partir de su clave pública, resolviendo el problema de
la factorización de grandes números que es clave en el algoritmo RSA que se
usa para encriptar las claves de sesión.
|
|
13.- PGP práctico, como se usa un keyring
|
Supongamos qué ya instaló el PGP en su computador y creó
exitosamente su par de claves privada y pública (el proceso es bastante
intuitivo como para que lo obviemos en esta explicación), por experiencia
propia, lo que más me costó entender fue el uso del keyring (llavero) llamado
"PGP keys" que queda instalado en el tray del sistema, por ejemplo mi
llavero es algo así:
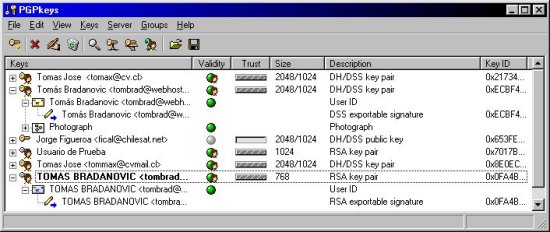
Lo primero en extrañarme fue una
cantidad de claves de gente que yo no conozco que aparecían en el
llavero, partiendo por la del propio Phillip Zimmermann y de varios
empleados de Network Associates la empresa que distribuye el PGP (las
borré todas ¿para que tener claves de personas con las que no
intercambiare nada encriptado?). En la ayuda del
PGP (disculpe Mr. Zimmermann por el pirateo) aparece el significado de los
iconos que es lo que se muestra a continuación:


En realidad lo único que me parece relevante aquí es que
las claves que tienen una barra con líneas diagonales indican que en el
llavero está el par completo de clave pública y privada, las demás son
solo claves públicas. Algunas operaciones útiles son Keys, Import (para
agregar al llavero una clave pública que esté en texto ASCII por
ejemplo), Keys, Add (para agregar una foto a nuestra clave pública), Keys,
New key (para crear un nuevo par de claves). En verdad el uso del PGP es
bastante intuitivo.
Si después que generamos un nuevo par de claves no nos
aparece la barra con diagonales en el llavero entramos a Keys, Key
propierties y le chequeamos el casillero "implicit trust"
como muestra la figura:
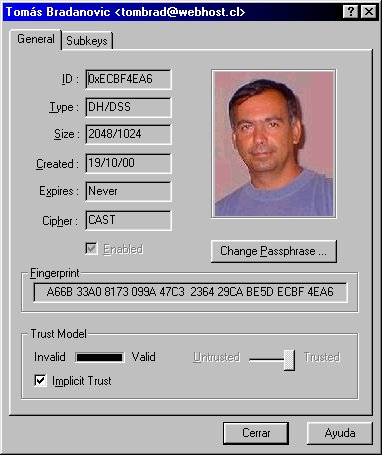
Esta clave pública de 2048/1024
bits (con foto incluida) se puede traspasar a un archivo ASCII, con lo que
se convierte en::
-----BEGIN PGP PUBLIC KEY BLOCK-----
Version: PGPfreeware 6.0.2i
mQGiBDnvt9gRBADbuYXMcdZal3cfOqmaMemMCXnE0UYniXFbAhDxx9Uw5sYqyo14
6s28+kzFwm3k8GAewBw8YuME3+sYDschZ8GnNVDwjE1FffKSpEe+aE8IRQ34CFu0
tdjvMvTRn8coTWvjG7Yu+vcry73ACIdqPI67EYwV/uXY8gQm7eWnfruiSwCg/+WK
EXu7czMqY02b1KMUPD03kSED/1Rj5G6vwRAKorBglTDX+52k2DnNl7Sx2GC7EQQc
fpH2xYctFr2a9fVffjWO9VCqGd6CLxJXKt6oN0b73lFBgZGyZsFLGvaUHfoATf/b
qi7O1Rto3rVf2NhLXdQF//qRRhYbvc4CBCPHBQAKRLRckKfXoD5j4ZzIii0CMCQr
mDnGA/9KwgueEf0105tLnHXXbEsAUitVaZi/kc2jDPPfze0+sIDxSNe27Nrn5JGN
U/ZIEy+pk07oi9ydkTjiJWeih5kUt/gDwfEyp02q6hQ14lnq0M1wUQVNoqJ2q7ic
Gn9C4aJYr/Q6tmPlDkEFOzDtgnJcf6jmrEvHUDIWYQfvmg4QFbQlVG9t4XMgQnJh
ZGFub3ZpYyA8dG9tYnJhZEB3ZWJob3N0LmNsPokASwQQEQIACwUCOe+32AQLAwIB
AAoJECnKvl3sv06maa4AnjpQGrtt8LaeOZkzx4yzqUP9TEXDAJ0UxRSeZlQ5ND36
XtMuq2n6+MbcgrkCDQQ577fZEAgA9kJXtwh/CBdyorrWqULzBej5UxE5T7bxbrlL
OCDaAadWoxTpj0BV89AHxstDqZSt90xkhkn4DIO9ZekX1KHTUPj1WV/cdlJPPT2N
286Z4VeSWc39uK50T8X8dryDxUcwYc58yWb/Ffm7/ZFexwGq01uejaClcjrUGvC/
RgBYK+X0iP1YTknbzSC0neSRBzZrM2w4DUUdD3yIsxx8Wy2O9vPJI8BD8KVbGI2O
u1WMuF040zT9fBdXQ6MdGGzeMyEstSr/POGxKUAYEY18hKcKctaGxAMZyAcpesqV
DNmWn6vQClCbAkbTCD1mpF1Bn5x8vYlLIhkmuquiXsNV6TILOwACAggAudvP62rs
7rGRuWSMTiTzEckZMifLCqAv15V6VjLVEjnFRUi/43hCIBKOKkHiGHUVhHfjc22h
wZZIVw+NsMJtdOFfYM8/KT4tYYZy02vRcIfY77dxj/Dz3Ewrf4Dw5ee5S/nBKQvZ
xw6KbMaAdayMaO/sN8eicECwpO2z3ZMLIEuUNed8Cmgm8/AzDbSWicYAfrrWtEki
mQutI1ttNpjgpR89ahKRUXx4S5u5cOQV33i+W1QwyaNmc4zxk6A0LXfhDnVZCUsP
GgZ5MPQ1fhFBJRLjIjmkMMq8Nhp5bp8sHwMs1dFK3wA7deyFoE9UeziLOLb4lBqM
46Vq4lCbQ8bkEYkARgQYEQIABgUCOe+32QAKCRApyr5d7L9OpmtxAKCRI9C3jGLg
mxWqnS9iYJ+HfbjUCQCgk5M7HFZLpG4T/FF+NHfnAFw72JQ=
=wLGv
-----END PGP PUBLIC KEY BLOCK-----
El archivo ASCII se puede enviar en el cuerpo
de un e mail, el que la recibe la copia al notepad y la importa con keys, Import
Mi otra clave pública es de 768 bits
lo que la hace mucho más corta, además es compatible con versiones del
PGP para DOS:
-----BEGIN PGP PUBLIC KEY BLOCK-----
Version: PGPfreeware 6.0.2i
mQBtAzg78rcAAAEDAKwCJYL7IJZl+dsJ2EvC8Ii/YsVYmjASNjgQK9buKmq2Zms2
T/vTFAoRi6Gw1dtZ1L+pZN1yKd3iYu0hEp0uUzABX59EYjB2Y0kSsoBTG+7yEQ9n
rUwepu3gHyJ2D6S1pQAFEbQlVE9NQVMgQlJBREFOT1ZJQyA8dG9tYnJhZEB3ZWJo
b3N0LmNsPokAdQMFEDg78rrgHyJ2D6S1pQEB14QC/i+7vF7kbmZ4AttQ6s5EoLt4
4cjB/5Viw45iyIBkbsmmww11Oh7srcwvxvHPugIlm/xiEG7kg+EQuxkB0k2bRPbP
Qx2FfM8QRyiMbkv6gnDcuqSE+FfXmMXAnfxtwx6UKA==
=Oopq
-----END PGP PUBLIC KEY BLOCK-----
Cuando encriptamos un mensaje y lo
empaquetamos en armadura ASCII queda algo más o menos así:
-----BEGIN PGP MESSAGE-----
Version: PGP 6.0.2i
qANQR1DBwU4DKkRM7vetPh0QCACSDygYk29v6I2kTGimsUk8Yn6O4jiHFfsk2hSa
pNxtnBf34JVt724ZSPg8RiACsbORdPx0CD955ueu760lqKzjhQ54cJs1Z8jQMdT3
8ChnRV3fJOa304X0e9//hPUzDqKCMiL2H00ZxmVhc4C+u0nvXJq2Tnwlsd2nBjUb
yEZmi+sLzlL8KCXrBCFgaY6paJFZQvpnupxGOLAoGqHerElxPFdUIxnHBvPFeInd
0RofQzlnMZPREQ7+O+5wGMlxI0E2lOG8jcFWcg8YCKFv9XIIyanxVJ2nLL40y7qD
5WJdt2w8SOMAaJ/pjgdTT6eiswDYqx9J5z4+TeTVAt0jMUs/CACUcrK4g0zCNPCU
tj8ydfq9EvlpI0rSztoAtxGyCYCNnoLiaVdugClseC++IyefIHpKxs4PH0xWBGPV
P1OgXp7thGRlzxuNYKog1M6LyNDrdllr/uzVWpuEmIRRExEtl8MKf2Sx77fXxO+G
NyhnsB27RYk1Z6N+6814Vu4DCj43QMGGowmzORu43t4RpcAjcnLjH0/qTxa9DugV
jnu9Mw2bbPi2Zy6lAodZjAzg1rfBPFhoacPL73XSJAbF85YJkUR8/tND694XpCZ6
646G8WbcKha2PwGkz0OsGxEEis8fwBBKjePofwOk46O3Dngl+cgfdSETyCcDBcYM
VmP+IzVzycJyoGGLtjOCk9RETvkV1jbz79kH/ND+EWtlrpv0Sz2UP0J1cXihBoso
xhEpDqHEgR1O6KaDMsPXwR075WqAbqhwgHGIjjcc7C52wKWigo/R8Cx/+f1RF9K2
YzbcWqKapO5vVehnHwWYQpj7/fec+Gcuw1eS+FacAaxrLwboQYcLLVIVQmt9ornf
Ra1fdcr9XMo1SSQherkIj4C1XRYD2pZj3YWUVO8t7TL8EvZXyLwXFBucI1xDfAtg
Y2iAA8R+Ll7cBkyPI3DdA1OIHUa1cKs67LCd+G0LzSzvl2A1nr80FK6VuCD8Uqng
QCDUaTqoiaqRTAgtdED3DrtqhFRz6m+wu+xq4EJdxwYAS11d79ViIzZx8KhEQUJo
HNEuOiaLMN2Uula7fYgBa9zpoZgf/BYDJPa6hP7yzRgZRXxJqfZg4jM068RnaWnt
Q/VnJQyBJNthb59MjLBukPkdwjSYojlPBkugoy6EpYboQZlz/jdpDfmCH1FQhPRp
cxqDQvf8zRMTrqdhAMrzR2gwyugF7T6mU6IzWWRDP1h1j+Tw/ZCWuwpQ7zZtIYgN
IDo7i9x9WarGcq2C4nDdm1wzqdW3R0mBxyy3hINeUxvlepg1sy0L4LjWBRHZBp1b
FEq+nawmNr+KT4OC78fwNyuaauQQUCC0N0tPKk8+mEyCa8eY2SpDeLMm4oYjmlNq
pqJKtsD3T98Qzowc31FLoAWFjAVoLKjlR+ljkghlTibf4R6BcLgmp+hfhRdnf/xb
Gc77dknjGv6Xg8is9qSc6jNq8nt4WpFwnmUrrduUfiZBK2guTK/qNPHDQ5fFu7H+
PxWPL49gN24fgAiXReoCggdJFBEkfJPmYRCkzRF1PYhfjlOYM1bAVmjfEPBmrqRF
Rn1MWT9dBeCt6jrsaKIxVQspPB6uXQKuI1xBX48CrLvHEPl02Q72ZqXxRasXV70Y
h+UnggO6Ha/S6WtU/dDU8psCm+LMSETG/OEW4vHJ0BygUtvkJ0X+jxwEMNgZwAKF
tearJEg0FcCRYd7782Gst57+RxxVBEf0V9w4U5dP4n5EOUDy5NQR2R0nE6nL7QPq
4AJI9iEZmFyBM/8=
=JOYJ
-----END PGP MESSAGE-----
La ventaja de tenerlo es ASCII es que
puede copiarse, cortar, pegar en el notepad, inclusive podríamos copiar
el texto escribiéndolo letra a letra o leerlo con un OCR y, por supuesto
enviarlo en el cuerpo normal de un e-mail
|
|
14.- PGP para DOS y para Windows
|
Las dos versiones más populares del PGP son la
2.6i para MS/DOS y las versiones 5x a 5x para Windows. La versión para DOS
consiste únicamente en un pequeño programa .exe y funciona con argumentos de
línea de comandos, por ejemplo con instrucciones tales como:
pgp -e <archivo_a_encriptar> <identificador_clave_destino>
Un listado completo de comandos para PGP 2.6i puede
verse en Conceptos básicos sobre el PGP. La ventaja de esta versión es que resulta muy fácil
hacer funcionar al PGP desde dentro de otro programa, ya que pueden enviarse los comandos por
una función tipo shell o algo por el estilo.
La desventaja del PGP 2.6xi es que solo trabaja con
claves cortas y algoritmos actualmente considerados débiles, a pesar de ello
para ambientes donde no abunden los code-breakers esta es una versión
todavía bastante segura, siempre y cuando se use correctamente.
El PGP 5xi - 6xi para Windows no trabaja con línea de
comandos así es que si queremos usar sus funciones desde dentro de otro
programa tendremos que usar DLLs especiales como las PGPDLLS.ZIP que se
encuentran en mi Sitio de Descargas
|
|
15.- Usando PGP con criptografía convencional
|
Algo que me intrigó por un tiempo fue la
opción del PGP de usar "criptografía convencional", es decir
usando la misma clave a ambos lados para encriptar y desencriptar el mensaje.
¿Cual era la idea de usar tal opción?
En pocas palabras si conocemos a la persona con que
vamos a intercambiar mensajes y tenemos acceso personal para ponernos de
acuerdo en un párrafo secreto (hablando personalmente, sin transmitir ese
párrafo por ningún medio), el cifrado convencional es, lejos, mucho más
seguro que la transmisión usando la clave pública. esto elimina las
debilidades del RSA y la posibilidad de averiguar la clave privada por algún
(improbable) algoritmo desconocido que permita factorizar grandes números.
El uso más seguro del PGP sería entonces poniéndose
personalmente de acuerdo con la otra parte en un párrafo secreto común,
usando criptografía convencional y firmando el mensaje con nuestra clave privada
|
|
16.- La seguridad no se basa en secretos
|
En la época de la criptografía clásica la seguridad
se basaba en mantener el algoritmo o el dispositivo encriptador bajo el más
estricto secreto. Con el tiempo esto demostró ser una muy mala política, a
Alemania por ejemplo la creencia de que su máquina encriptadora
"Enigma" no era conocida le dio un falso sentido de seguridad que
permitió a los aliados conocer sus comunicaciones en clave desde el principio
de la guerra.
Otro ejemplo de antología es la "clonación"
de los teléfonos celulares; a las 48 horas de descubrirse el algoritmo
"secreto" empleado por los GSM, lo que obligó la migración a
la tecnología a PCS a escala mundial
Los secretos son difíciles de guardar y cuando hay
muchas personas involucradas, guardar un secreto es tarea casi imposible. La
criptografía moderna (es decir la de la época de los computadores) usa
algoritmos conocidos por todos, los algoritmos se difunden a toda la comunidad
interesada en el tema de manera que puedan ser sometidos públicamente a toda
clase de ataques, ahora la situación se ha invertido y para el que logra
romper un sistema le resulta muy difícil mantenerlo en secreto.
Por ejemplo tal como vimos en las secciones anteriores
el algoritmo usado por PGP es conocido por todos, y no solo eso, el propio
código fuente del programa está disponible para quien se interese en
analizarlo, puede bajarse de Internet libre y gratuítamente. ¿Como puede ser
el PGP un sistema tan seguro si cualquiera conoce su funcionamiento?.
La respuesta está en el nuevo enfoque introducido
a la criptografía desde la aparición de los computadores: la seguridad ya no
se basa en el algoritmo mismo sino en encontrar funciones matemáticas
irreversibles, que no tengan solución conocida como es el caso de la
factorización de grandes números. Los nuevos métodos dependen más de la
investigación y el avance científico que del conocimiento de alguna clase de
"secreto"
|
|
17.- Criptografía no es igual a seguridad
|
Este es un punto muy importante de entender, la
criptografía es un subconjunto de algo mucho mayor; la seguridad
informática, Tener instalado el PGP no soluciona problemas de seguridad
en las estaciones de trabajo.
Cualquiera que tenga libre acceso a nuestro PC donde
están los archivos secring.skr y pubring.pkr podría, por dar solo un
ejemplo, sacarles copia, instalarlos en su propio PC y usando un poco de
"ingeniería social" averiguar nuestro párrafo con lo que nuestro
(supuestamente) perfecto canal confidencial, ya no valdría nada. PGP protege
nuestra confiabilidad mientras los mensajes encriptados viajan por Internet,
ni antes ni después por lo que no debemos confiar ni menos descuidar el
acceso de extraños o potenciales atacantes a nuestros PC.
PGP, tal como cualquier otro esquema criptográfico, parte
del supuesto de que la integridad física de la información en el equipo está
asegurada, que nadie tendrá acceso al disco donde se guardan los keyrings,, el
randseed, que nadie podrá copiar o apropiarse de algún modo de estos archivos
(por ejemplo si el equipo está conectado en red, si se tiene acceso a archivos
swap, si se tiene equipamiento para captar e interpretar la radiación
electromagnética emitida por el computador, etc.)
Entre las medidas de seguridad informática posibles
estaría la creación de una partición encriptada del propio disco duro
usando (como no) PGP Disk.
|
|
18.- PGP Disk
|
Un problema de seguridad clásico de Windows 95, 98 y ME
es que no tienen forma de restringir el acceso a los directorios. Existen
muchas utilidades como Magic Folders, Candado etc. que permiten ocultar
carpetas pero la verdad es que ninguna de estas resulta muy satisfactoria ni
menos segura en términos de encriptación, de hecho para casi todas estas
utilidades podemos encontrar programas que permiten crackearlas. Dentro
del paquete freeware PGP 6.xi que se puede bajar de http://www.pgpi.com
se encuentra la utilidad PGP Disk que permite crear volúmenes encriptados
y, entre las medidas de seguridad informática que protegen al disco de
acceso no autorizado, esta es la mejor que conozco. PGP
Disk simplemente encripta un espacio del disco y crea un archivo llamado PGP
Disk volume donde podemos guardar nuestros archivos sensibles fuera del
alcance de intrusos. El volumen usa un método de encriptación fuerte (de
grado militar) llamado CAST (el mismo algoritmo simétrico que se usa
por defecto en el PGP normal). Para "montar" el volumen se debe
entrar el párrafo que le hayamos asignado, una vez montado para todos los
efectos prácticos el volumen PGP disk se comporta tal como si se tratara de
una nueva unidad de disco, con su propia letra, carpetas etc. Algunas
características interesantes son que además del párrafo principal podemos
asignar párrafos de acceso secundario, así varias personas pueden tener
acceso al volumen usando un párrafo distinto y personal. Sin embargo el
poseedor del párrafo maestro podrá administrar, permitir o negar accesos a
los párrafos secundarios. Además podemos asignarle
claves públicas de PGP a un volumen, de manera que el poseedor de los
párrafos de esas claves puedan tener acceso al volumen. Algunas
aplicaciones útiles del PGP Disk pueden ser para respaldar nuestros archivos
confidenciales en alguno de los lugares de la web que nos ofrecen ese
servicio, para mantener nuestros archivos confidenciales dentro de un ambiente
de red, para proteger el acceso no autorizado a nuestro disco duro (o parte de
el) etc. Importante:
aunque es prácticamente imposible que alguien que no tenga el párrafo pueda
ingresar a un volumen encriptado si podría borrarlo, recuerden que se
trata simplemente de un archivo.
|
|
19.- Secure Socket Layer (SSL)
|
El protocolo SSL es el que funciona cuando en el explorador
de Internet aparece el mensaje "Esta entrando a una sesión de
comunicaciones seguras" o bien aparece un símbolo con un candado cerrado.
Se trata simplemente de una codificación trasparente para el usuario que
efectúa el browser (Explorer, Netscape, etc.) antes de enviar los datos por
Internet, al llegar a su destinoi también son desencriptados de manera
transparente.
Una sesión SSL comienza con una etapa de saludo (handshaking)
donde se generan las claves de sesión y luego una de comunicación sonde se
envían los datos encriptados. Debido a las restricciones legales en USA los
exploradores usan claves de solo 40 bits para sesiones SSL, lo que constituye
una notable debilidad en la seguridad de la comunicación. El SSL se usa
principalmente para evitar que información como los password por ejemplo,
viajen por Internet abiertamente, al alcance de cualquiera que tenga acceso a
los servidores.
|
|
20.- Esteganografía
|
La esteganografía o uso de canales subiliminales consiste
en esconder información dentro de otra aparentemente inocente, por ejemplo
dentro de una imágen de bitmap que represente un paisaje bien podríamos
ocultar un texto secreto u otra imagen confidencial
por ejemplo.
Una técnica empleada para ocultar la información
consiste en cambiar el bit menos significativo en algunos puntos de
la imagen , así los puntos cambiarían su valor en solo una unidad lo que resulta
indetectable al ojo humano (como los colores se representan por números el
color 850 por ejemplo es casi idéntico del 801), los puntos que se cambian se
escogen al azar con un generador de números seudo aleatorio, y la semilla de
este generador se determina a partir del password. Finalmente antes de
diseminar la información en la imagen "portadora" es encriptada lo
que aumenta la dificultad de recuperar sin conocer el password.
La limitación es que la imagen portadora debe ser a lo
menos 8 veces mayor que la información que deseamos ocultar. Otra limitación
obvia es que si cambiamos o editamos la imagen de algún modo perderemos la
información que estaba oculta en ella.
El procedimiento mencionado arriba es usado por el
programa esteganográfico llamado Winhip.exe que es freeware y puede bajarse
de mi Sitio
de Descargas
|
|
21.-Otros Artículos Sobre el Tema
|
En este mismo sitio hay varios artículos relacionados
con el tema, esto son:
|
|
22.- Créditos
|
Este artículo debe gran parte de su contenido
(en verdad la parte sobre teoría de información es un plagio simplificado) al libro "Criptografía y Seguridad
en Computadores" de Manuel José Lucena López. El libro completo, sin ningún tipo de restricciones o cortapisas,
puede ser descargado TOTALMENTE GRATIS desde:
http://www.kriptopolis.com/libro.html
Una nota adicional sobre http://www.kriptopolis.com
: Es uno de mis sitios favoritos sobre seguridad informática y criptografía,
los temas se tratan de manera informal y simple tal como a mi me gusta y no hay
estúpidos hAckErz exhibiendo su indecente egolatría, solo gente interesada en
los temas de seguridad. He encontrado mucha información útil allí y lo
recomiendo de verdad
También saqué información (y un par de
snapshots) de la propia documentación del PGP que viene junto con el programa,
además del FAQ sobre PGP escrito por Arnoud Engelfriet
Pido disculpas de antemano por haber omitido las comillas donde corresponda.
|



